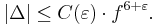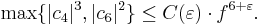Szpiro's conjecture

In number theory, Szpiro's conjecture concerns a relationship between the conductor and the discriminant of an elliptic curve. In a general form, it is equivalent to the well-known abc conjecture. It is named for Lucien Szpiro who formulated it in the 1980s.

The conjecture states that: given ε > 0, there exists a constant C(ε) such that for any elliptic curve E defined over Q with minimal discriminant Δ and conductor f, we have

$\vert\Delta\vert \leq C(\varepsilon ) \cdot f^{6%2B\varepsilon }. \,$

The modified Szpiro conjecture states that: given ε > 0, there exists a constant C(ε) such that for any elliptic curve E defined over Q with invariants c₄, c₆ and conductor f, we have

$\max\{\vert c_4\vert^3,\vert c_6\vert^2\} \leq C(\varepsilon )\cdot f^{6%2B\varepsilon }. \,$

References

Lang, S. (1997), Survey of Diophantine geometry, Berlin: Springer-Verlag, p. 51, ISBN 3540612238
Szpiro, L. (1981), "Seminaire sur les pinceaux des courbes de genre au moins deux", Astérisque 86 (3): 44–78
Szpiro, L. (1987), "Présentation de la théorie d'Arakelov", Contemp. Math. 67: 279–293

External links

Szpiro and ABC, notes by William Stein